Venezuela’s 1 million percent inflation and other realities of exponential growth
Venezuela’s financial implosion is devastating. People are starving. The government is printing money to cover budget gaps. And the IMF estimates that inflation will top 1 million percent.
But what would it take to get 1 million percent inflation?
Before reading on, take this poll. (If you know the formulas for compounding, please don’t use them . . . just make an intuitive guess.) Then scroll down to see the correct answer.
.
.
.
.
.
.
.
.
.
.
.
.
.
The correct answer is around 2.5%.
This seems to make no sense. Imagine that you had $100 and put it in the bank. 2.5% of $100 is $2.50. So if you got 2.5% interest on the $100 every day, at the end of a year you would accrue $2.50 times 365 days, which yields $913. You’d end up with $1,013, which is a nice haul, but not a million times what you started with.
Of course, I have been ignoring the compounding. If you get 1% interest per year, the compounding is trivial. But if your money loses 2.5% of its value every day, the compounding is brutal.
For mathematical types, the formula for compounding daily is this:
![]()
To find out what the price of a commodity is at the end of the year, you multiply the price at the beginning of the year by the annual rate. Seems simple enough: a 1 bolivar cup of coffee with 2.5% annual inflation costs 1.025 bolivars at the end of the year. But when that cup of coffee goes up by 2.5% every day, things get way out of hand.
For example:
- 0.01% daily inflation = 3.7% annual inflation
- 0.1% daily inflation = 44% annual inflation (that cup of coffee costs 1.44 bolivars, and your money has lost 31% of its value)
- 1% daily inflation = 3678% annual inflation (the coffee costs 38 bolivars, and your money has lost 97% of its value)
- 2% daily inflation = 138,000% annual inflation (coffee costs 1,380 bolivars, and your money has lost 99.9% of its value)
- 3% daily inflation = 4.8 million% annual inflation (coffee costs 48,500 bolivars, and your money has lost 99.998% of its value)
At even 1% daily inflation, which seems quite tame, the currency rapidly becomes nonviable. No one wants to get paid in bolivars, they’d rather get paid in coffee. You have a barter economy, or one where people get paid in dollars or euros or gold or anything whose value remains relatively stable (not bitcoin).
This is really happening, here’s the cost of a cup of coffee as estimated by Bloomberg:
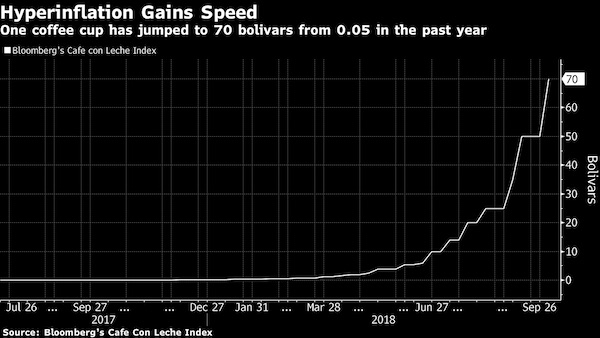
Stop the cavalier talk about exponential growth
There are obvious lessons here about government trust and what happens when deficits get out of hand, but I won’t be going there.
Instead, I want to talk about exponential growth.
Exponential growth is beyond human intuition. You can do the math and find out that a 1% increase every day generates a 37-fold increase in a year, but that still defies your intuition.
A useful tool to extend that intuition is the rule of 72. Divide the 72 by the percentage rate, and you get the number of periods it will take for something growing exponentially to double.
Let’s switch from daily and yearly to monthly for this example. Suppose you have a social Web site whose numbers are growing by x% per month. How long does it take for the site’s membership to double?
At 1% per month, 72 months, or 6 years.
At 2% per month, 36 months, or 3 years.
At 3% per month, 24 months, or 2 years.
At 4% per month, 18 months, or a year and half.
At 6% per month, the site’s membership will double in a year.
And at 12% per month, it will double in half a year.
This is my pet peeve when you hear that sales of Apple’s iPhones, or members of TikTok, are growing exponentially. It means absolutely nothing.
A growth rate of 0.01% per month is exponential growth, and will yield a doubling in 600 years. Yes, that’s exponential, and no, it’s not impressive.
A growth rate of 12% per month means it will double every 6 months, and if the rate holds up, will grow by a factor of 900 in 5 years. That’s massive.
Both are exponential growth. Which is why exponential growth means absolutely nothing.
Beyond that, growth rates are highly variable and, if they are significant, always hit a barrier. Venezuelan currency can’t keep going into trillion bolivar bills and losing 99.998% of its value every year — people will give up on it. Facebook’s membership can’t grow beyond the population of the planet. When you are looking at growth, you’re typically looking not at ordinary exponential growth, but at a logistic growth curve (also known as an S-curve or learning curve) that ramps up rapidly and then levels off at some point. A typical growth curve looks like this:
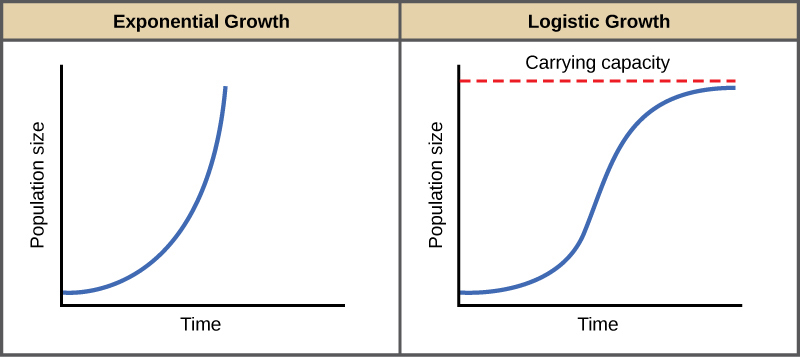
Look at the curve on the right. It looks like an exponential curve, then it looks like linear growth, then it levels off. It’s very hard to accurately estimate the growth rate at the beginning. And whatever that rate is, it’s even harder to determine where and when it will level off.
So the pedant in me pleads with you: stop colloquially talking about growth being “exponential.” Without knowing the rate, you’re not actually saying anything. And even if you do know the rate, growth rates build in a way that confuses people’s linear minds. So without precision, your description is about as valuable as a Venezuelan bolivar.
One of my favorite quotes:
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”
― Albert Einstein
Einstein, an amazing reference mister Simon !
Have a nice day !
In 2008, hyperinflation in Zimbabwe reached 79, 600, 000, 000% per month. One $US was worth Z$26 billion in local currency. I bet you can have some fun with those numbers.